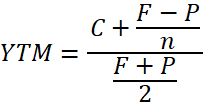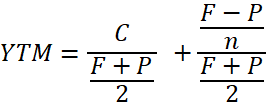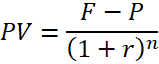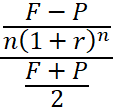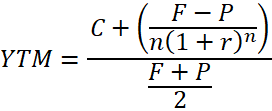It is time to admit it: the investment advice I gave in my book Investing in the New Normal (2010) is entirely outdated. Even worse, it is ineffectual. Not that putting your money into investment funds – the main focus of the investment advice there given – is guaranteed to lose you money. It’s just that it’s not really an investment, but rather a simple gamble that others will likewise put their money into the same “investment” vehicle and so make the price of that investment vehicle rise, enabling you to recoup your “investment.” But this is not really investing, at least not in the real economy. The money we put into things like stocks and investment funds is money that circulates entirely in the financial market, insulated from the real market.
As such, the approach I then advocated does not take into account the realities of markets. Of course, that is quite a charge to lodge against my book or any other of the plethora of investment guides available on the market today. But this critique holds true for virtually all of them. They all partake of the same error, as did mine: the failure to take into account the realities of markets, to wit, the failure to distinguish between the real market and the financial market.
The usual approach is to view the market economy as one big market with various submarkets: commodity, real estate, retail, various financial submarkets, etc. And when we invest in things like mutual funds we are investing in these sectors of the real market. This is a fundamental error. In reality there are two overarching markets which are separate from each other and run in separate circuits, insulated the one from the other.
I developed this understanding while working on my history of money (Follow the Money, 2013) and the translation of Joseph Schumpeter’s Treatise on Money (2014). In the process I also discovered the work of the entirely overlooked Spanish economist Germán Bernácer, who made this dichotomy of the two markets the basis of his framework for economic understanding. For an introduction to this approach to understanding economics, consult the series of articles published under the title The Two Markets elsewhere on this website.
Now then, this discovery eventually led me to divest our portfolio of stocks and funds, as I had no wish to continue life in the casino. Which left us without much more than savings accounts earning minimal interest.
It was then that I discovered a hitherto untapped investment vehicle – the humble corporate bond. With bonds, the main objections to investing on the financial market are lifted. The bondholder has a direct connection to the company the bond of which he holds, for he receives periodic interest payments from the company which are contractually agreed upon from the start, and he receives the full amount of the bond’s face value from the company when it falls due. At least, that is, if the company issuing the bond does not redeem it ahead of time, which is one of the few risk factors involved, or if it engages in debt restructuring or goes into bankruptcy, neither of which, thankfully, happens very often.
The great thing about bond investing, then, is that it provides you with reliable, predictable revenue streams direct from the company, thus unaffected by the vicissitudes of the financial market. In fact, when you buy a bond, you can nail down two income streams which are contractually fixed, the value of which you can calculate at the time you purchase the bond, and which will come to pass unless, of course, something catastrophic happens.
The ability to calculate the value of these two income streams is fundamental. So let’s figure that out.
When you analyze a bond, the first thing you realize is that it pays interest, at a fixed rate, which is known as the “coupon.” This term derives from former days when bonds were purchased in the form of paper certificates with dated coupons attached. In order to receive your interest payment, you cut out the appropriately-dated coupon from the certificate and submitted it to the issuer or its agent, a bank or other financial institution. This is also where the rather denigrating term “coupon-cutter” originates; it refers to people who do not do any work but instead live off of interest income.
At any rate, the coupon is one source of income from a bond investment. But not the only one. There is also the differential between the face value of the bond and the market price. Because bonds are bought and sold on the financial market, their value fluctuates. When they are initially issued, their value is known as par; for example, a bond issued (in dollar terms) for $100 has a par value of $100. If the value drops below $100 (which is often the case) then you will have another source of income if you chance to buy it at that lower price, because upon maturity you will receive the face value back. Of course, the reverse is true: you will lose money if you buy a bond at a higher price than par and hold onto it until maturity.
We will try to capture these two income streams in a formula that can be used to calculate the present value (what it’s worth to you now) of a bond generating these various streams. This is called yield to maturity.
The standard formula used to calculate yield to maturity is
Where
- YTM: yield to maturity
- C: coupon
- F: future bond price (value at maturity)
- P: bond purchase price
- n: years to maturity
A closer look reveals to us that this formula captures the two separate income streams in one equation. We therefore can break this formula into two parts:
The first part has to do with the coupon income, the second with the value of that differential between purchase price and par value.
The first part of the equation is an attempt to calculate the present value of the series of interest payments that we will be receiving. As such, it provides a definition for yield over time. Yield at any particular point in time is the coupon divided by the bond price. So, for example, if the coupon for a bond at the time of purchase is 5%, and the purchase price is $70, we divide the coupon by the price, which gives us 7.14%, which is the bond’s yield. Now then, since we are dealing with a series of coupon payments, we take the coupon and divide it by the average of the price at maturity ($100) and the price at purchase (for example $70), thus $170/2, leaving $85. This gives us 5%/85 or 5.88%. It is an average of the yield over this period.
The second part of the formula deals with the differential between the present and future (final) price of the bond. Given a future price (at maturity) of $100 and a purchase price of $70, what is the value today of that $30 that you will be pocketing upon maturity, for example, five years from now? This formula takes that $30 and divides it by the 5 years to maturity, yielding 6, and then divides this by the average price of $85, yielding an average return per year of 7.06%.
So putting it together, given a coupon of 5%, we get 5/$85 or 5.88% as an average yield over time, and added to this we have $6/$85 or 7.06% as an average return per year on that $30. Adding the two gives a yield to maturity of 12.94%. That is the value the bond is generating per annum to you. At least, according to this approximate formula.
In this approximation, we take initial and final prices and divide them by 2. The assumption, thus, is a straight line progression for the bond price, while in reality the price will be fluctuating. But we can make adaptations to the equation so as to gain a closer approximation to the actual yield to maturity.
The first part makes the assumption that the nearer the time approaches to maturity, the closer the price of the bond will approach face value, and so it takes an average as an approximation. Of course, no one knows how the price will develop over time. It could appreciate earlier, making its value today greater, or appreciate later, making its value today lesser. Since we don’t know this, we have to make do with the “divide by two” approximation.
The second part, it seems, is more amenable to improvement. The above equation takes the capital amount that will be gained upon final payment, in this example $30, and averages it using the initial and final dates. But we can take advantage of the standard formula already in use to calculate the present value of any sum to be received in future. That formula makes use of a discount rate. It runs as follows:
Where
- P: present value
- F: future value
- r: discount rate
- n: number of years
If we take this formula and apply it to the second part of our equation, we have
When we combine the two parts again, we end up with this formula:
Where F-P is the differential, in our example $30; r is the rate of discount; n is the number of years to maturity, in our example 5; and (F+P)/2 is the $85 mentioned above.
As such, we have added a discount rate to the equation. This allows us to prognosticate for various inflation scenarios. We can sketch various scenarios, using discount rates of 3% (low inflation), 5% (higher inflation), and 7% (even higher inflation). This yields the following three results:
- 3%: 11.97%
- 5%: 11.41%
- 7%: 10.92%
As can be seen, these results are all lower than the standard equation given above, which yielded a result of 12.94%. It must be kept in mind that all of these results are approximations. The various inflation scenarios are useful to figure out best-case and worst-case scenarios.
It is also evident from this formula that low inflation is favorable to bond results, and disinflation or deflation is even more favorable. This is one reason why, during the time of the gold standard, bankers had no problem imposing deflation: it was great for creditors! Take our example here and furnish it with a discount rate of -3%, and the result is no less than 14.1%!
From all of this it is clear that bond investments provide predictable outcomes with clearly indicated interest rates, time to maturity, and value at maturity. This is why I recommend corporate bonds with an investment-grade credit rating as both a safe and a reasonably lucrative investment.
Now that I mention it: credit ratings form a topic that merits further scrutiny. Others include government bonds and bonds denominated in different currencies. But these will have to await another opportunity.
